
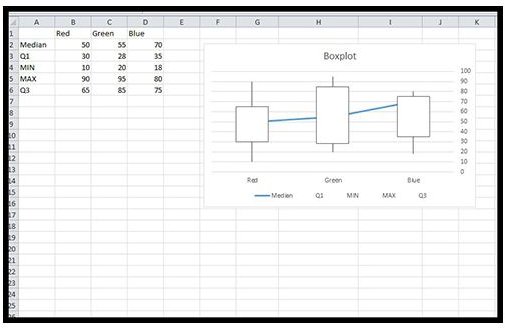
We get this result because Excel interprets the added means as stacked bar charts. When you press the OK button, the chart changes to that shown in Figure 4. Fill in the dialog box that appears as shown in Figure 3. This will bring up the dialog box shown in Figure 2.Ĭlick on the Add button (on the left side of the dialog box). We use the following array formulas to calculate the values for Lower (i.e. The Q1, Median, Q3 and Mean values for Brand A in the range F12:F17 are calculated by the formulas =QUARTILE(A4:A13,1), =MEDIAN(A4,A13), =QUARTILE(A4:A13,3) and =AVERAGE(A4:A13). To create this box plot manually, you need to first create the values in range F12:F17.
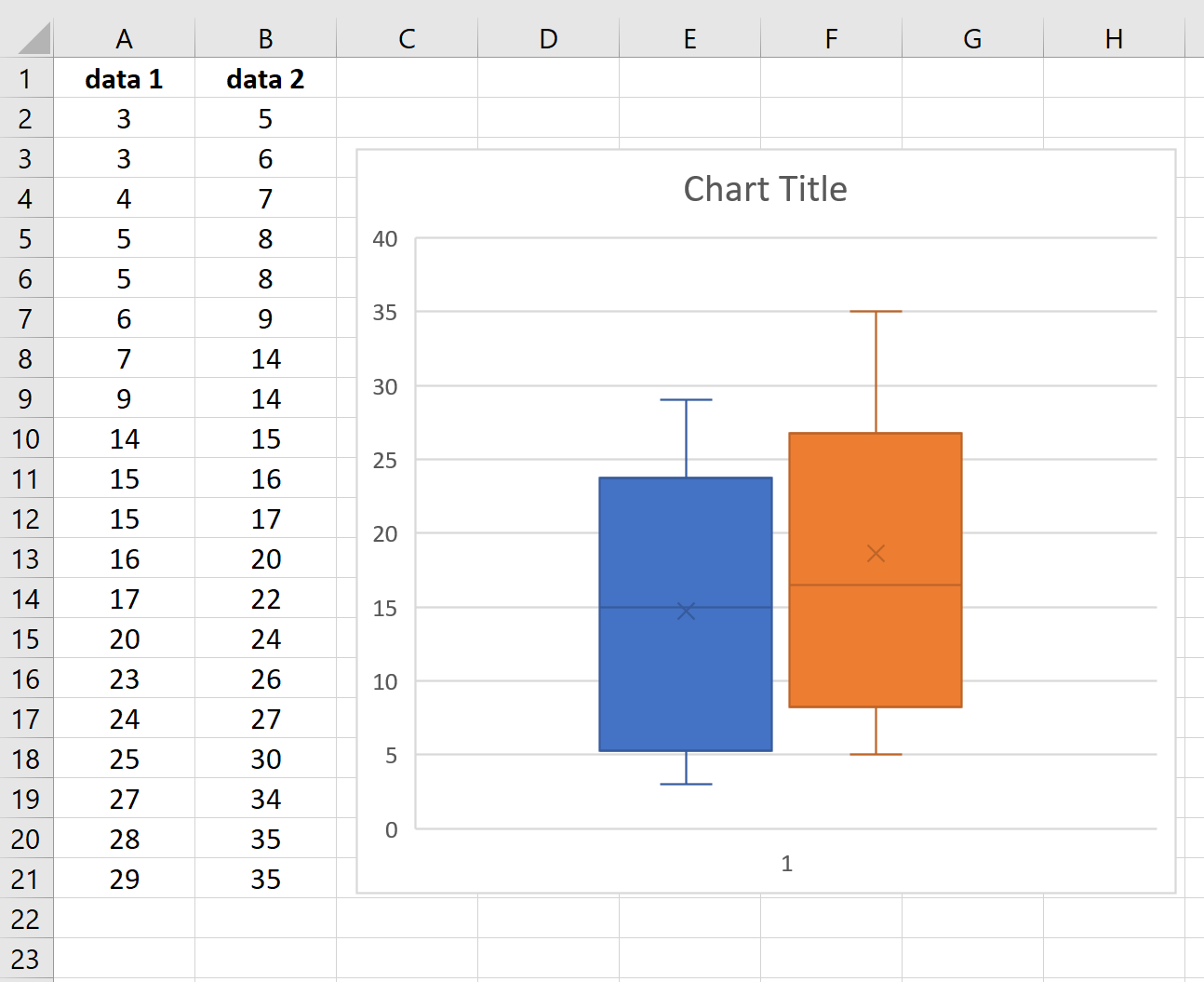
We now show how to construct this output manually using standard Excel capabilities. ExamplesĮxample 1: Repeat Example 2 of Special Charting Capabilities, showing outliers. The other difference is that we need to manually add a small circle or each data value greater than Q3 + 1.5*IQR or less than Q1 – 1.5*IQR. Similarly, the bottom whisker ends at the smallest data value greater than or equal to Q1 – 1.5*IQR. One key difference is that instead of ending the top whisker at the maximum data value, it ends at the largest data value less than or equal to Q3 + 1.5*IQR. The median of this data set would be 8.The procedure for manually creating a box plot with outliers (see Box Plots with Outliers) is similar to that described in Special Charting Capabilities. 7 + 9 equals 16, and 16 divided by 2 equals 8. In our example, you would take 7 and 9 - the two middle numbers - add them up and divide them by 2. What if the data set you're working with has an even amount of numbers? What if you had to find the median of 2, 4, 4, 7, 9, 10, 14, 15? You find the median here by taking the two middle numbers and finding their average.That's how we can be sure that it's our median. For the data set 1, 2, 3, 4, 5, the median number, 3, has 2 numbers before it and 2 numbers after it. In a data set with an odd amount of numbers, the median will always have the same amount of numbers on either side of it.
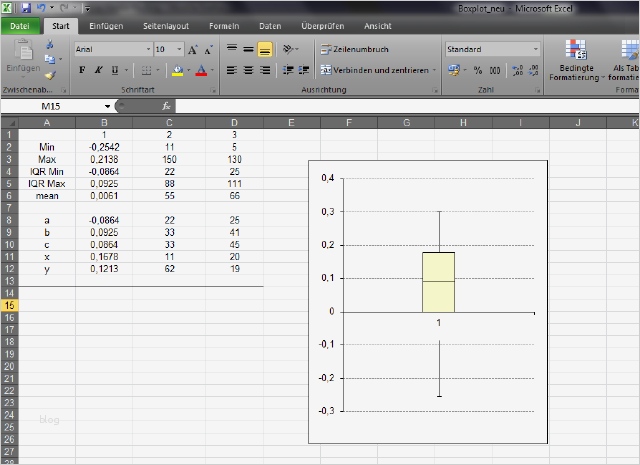
The median is also called the second quartile. (This is why we lined up all the numbers in Step 2.) For the data set in our example, 3 is the number that's exactly in the middle, and therefore is our median. The median is the middle number in the data set when the data set is written from least to greatest.


 0 kommentar(er)
0 kommentar(er)
